
INTRODUCTION
From the disintegration of the Darmstadt School in the early 1960s to the present, compositional practice has been defined by an incredible diversity of styles and techniques. One of the principal challenges to the theorist in analyzing this music is sorting through the multiplicity of approaches and determining which elements are of prime importance. The Sonatina for Solo Trumpet in three movements by Hans Werner Henze from 1974 is such a piece, incorporating a mix of tonal, atonal, and serial language. This study will expound on the variety of compositional techniques that Henze employs in his Sonatina for Solo Trumpet, and will argue that these techniques are all subordinate to processes described by the atonal set class (016). I will begin by looking at each movement separately and fleshing out the compositional language and formal features. At the end of each section, I will speak about the overarching importance of set class (016) in the movement. Finally, I will offer a few possible ways of uniting the disparate techniques used in the Sonatina.
Before delving into Movement I, it seems necessary to explain the musical examples used on this page. Many of the examples are generated using an online presentation tool called Prezi which require Adobe Flash in order to function correctly. To view an example, press the button labled “Start Prezi.” Once the example loads, you may use your keyboard’s left and right arrow keys to go forward or backward through the example. You will know that you’ve reached the end of the example when you are prompted to restart the example. In addition, all examples can be run in full screen and may be explored freely using the mouse to zoom in or pan around the viewing area.
MOVEMENT I
Compared to the other movements, the first movement of Henze’s Sonatina for Solo Trumpet, titled “Toccata,” is perhaps the most diverse in its use of compositional techniques. As a whole, it lacks a total commitment to tonality, atonality, serialism, or any other single process. And yet, this short, virtuosic toccata leaves the listener with the impression of a distinct form, rather than the shapeless amalgam that the theorist might expect. I propose that formal delineations in Movement I are generated through repetitive use of motivic material and a type of promissory foreshadowing that more will follow.
The large-scale structure of Movement I is comprised of five phrases of varying length separated by rests. Dynamically, these phrases follow the pattern loud-soft-loud-loud-soft. The opening material of the first phrase consists of ascending triadic or quasi-triadic figures interspersed with a single, persistent pitch. The reoccurring pitch at the outset is B♮4 and for ease of reference I will call this a pedal point. Therefore, we could say that the opening thirteen notes, defined as ascending triads with a pedal point, make up motivic material A. Motive A will be more specifically defined by its compound line and pitch content later in this study. The first deviation from this motive is a change in direction. Motive B has the broader definition as that which follows A and is more directionally flexible. Following motive B there is a restatement of both A and B, the first shortened and the second lengthened. The phrase ends with a new idea: ascending major and minor thirds resulting in a suspension and resolution. This final gesture is motive C. Example 1 shows these motivic ideas for the first phrase as well as the remaining phrases.
EXAMPLE 1: A formal description based on motivic material of Movement I from Henze's Sonatina for Solo Trumpet.
Some defining features of this aural interpretation of form are the repetition and imitation of motives A, B, and C. Of particular interest are the four suspension gestures that end a rhythmically active statement. The length of both the active statement and suspension vary in such a way to create the following time-domain proportion:
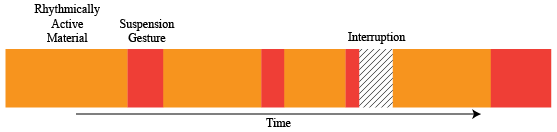
EXAMPLE 2: Proportional relationships among suspension gestures in Movement I from Henze’s Sonatina for Solo Trumpet.
The general effect of these proportions is a shortening of both the active material and the suspension following the first statement. After an interruption, the last suspension proves to be the longest, loudest, and highest.
Some interesting features of the form, as defined by motivic repetition, are sections of music that do not repeat. For example, phrase 3 has no basis in the preceding music and very little similarity to any music that follows. The best explanation is that rhythmic novelty of the repeated A♮3 acts as a foreshadowing of the coming movements, in particular Movement III. In addition, the descending figure at the beginning of phrase 3, while similar to motive B, resembles the opening gesture of Movement II. These distinctions cause this phrase to be marked for memory in such a way that the listener expects the composition to return later to these ideas.
One possible method of analysis of Movement I is by Roman numeral analysis. This assumes that the triadic figures present in phrases 1, 2, and 4 can be extracted from the compound line and have a clear harmonic function. In order to proceed, one must ignore the non-harmonic pedal points, sequences of ascending fourths, and occasionally incomplete triads. Given those exceptions, a tonal analysis of Movement I indicates that the piece is generally in the key of A minor, or the related key of D minor. Taking into account the influence of the pedal points and suspension gestures, some principal pitch classes emerge as marked for memory. Example 3 shows a partial tonal analysis and pitches that, due to emphasis, are marked for memory:
EXAMPLE 3: A tonal analysis of Movement I from Henze’s Sonatina for Solo Trumpet.
Due to the tonal relationships in phrase 1, where the resolution of the suspension gesture is the root of the tonic, I believe that all of the resolution pitches hold a degree of importance. Taken as a group, they constitute pitch class set [59T], member of sc(015). In a similar vein, the pedal point pitches taken together create pitch class set [E03], also a member of sc(015). On a middleground level of analysis, this prevalence of sc(015) is probably an intentional choice. As stated in the introduction, I believe that the entirety of Henze’s Sonatina is influenced on some level by sc(016). One may derive sc(016) by combining the two sets to create superset sc(0126), but this may be overreaching. I will return to the implications of set classes for the entire work at the end of this study.
Two more features of Movement I deserve mentioning. One is the use of ascending fourths in phrase 1 and 2. The occurrence in phrase 1 grows out of motivic material A and presents seven notes of the series in succession. The final two pitches, G♮5 and D♮5, are reversed and in the wrong octave. Phrase 2 completes the series with the exception of pitch classes C and F. However, it may be inferred that the preceding F♮4 and C♮5 could be interpreted as members of the same series of fourths. The other notable feature is the two whole tone sonorities that occupy phrases 3 and 5. Example 4 shows both the ascending fourths and whole tone characteristics:
EXAMPLE 4: Ascending 4ths and the whole tone odd scale in Movement I from Henze’s Sonatina for Solo Trumpet.
Both sonorities are members of the whole tone odd scale and both occur during motivic statements that point toward Movement II. In the final phrase, I believe this allows Henze to end Movement I without finality and leave the listener with the expectation of what is to come.
MOVEMENT II
The second movement of Henze’s Sonatina for Solo Trumpet, titled “Canzone,” is both literally and figuratively the central occupation of the entire work. On the one hand, it is saturated with atonal set class (016) on the surface and tantalizes the theorist with the hope of a Webern-esque, crystalline composition. On the other hand, Movement II proves to be the most freely composed of the work, obscuring any clear form or structural underpinning. I will first demonstrate the prevalence of sc(016) and related set classes on the surface before proposing some suggestions for background pitch-based structures.
The surface of Movement II has some strong connections with phrases 3 and 5 of the previous movement. The four-note figure at the start of phrase 5, for example, has a very similar set class as the first four notes of Movement II:
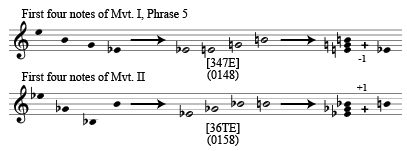
EXAMPLE 5: Set class similarities in Movement I and II from Henze’s Sonatina for Solo Trumpet.
While sc(0148) and sc(0158) are clearly different, their tonal construction of a minor triad plus a semitone creates an aural link between the movements. In addition, their melodic contour of a high pitch skipping down also encourages a connection. Furthermore, the general harmonic language of phrase 3 and 5 from Movement I is the whole tone scale. Here, too, one finds a strong corollary in Movement II:
EXAMPLE 6: Whole tone sonorities in Movement II from Henze’s Sonatina for Solo Trumpet.
The obvious difference between Movement I and II is the use of the whole tone even scale. A curious feature of the whole tone scale in Movement II is the link between the sonority and motivic elements. The whole tone even scale is linked to melodic descents, often comprised of alternating skips and steps, while the whole tone odd scale is only used in ascending lines.
The overwhelming majority of Movement II’s surface can be described as pitch class sets belonging to set class (016). Many instances of sc(016) are illustrated in Example 7:
EXAMPLE 7: Segmentation showing sc(016) of Movement II from Henze’s Sonatina for Solo Trumpet.
Not only are there a large number of incidental cases of sc(016), but there are examples of emphasized statements like the mezzo forte in system 3 and the fortissimo in system 5. I believe that these are clear declarations of principal material. One would hope that, for the sake of compositional conciseness, Henze would use pitch class sets belonging to sc(016) at all major moments in this work. Unfortunately, this is not the case. However, some of the other pitch material at work in Movement II can be derived from sc(016). Example 8 shows how one might transform sc(016) to create other relevant set classes:
EXAMPLE 8: A transformation of sc(016) into other set classes used in Movement II from Henze’s Sonatina for Solo Trumpet.
The set classes sc(015), sc(026), and sc(027) are related to sc(016) through a single transposition, and sc(025) is related by two transpositions. Taken together, all five set classes constitute the surface language of the movement. Also of interest, sc(027) when rearranged creates a series of ascending fourths. This was a motivic feature of Movement I. In light of this, sc(016) when similarly rearranged creates a “broken” series of ascending fourths where the top interval of a tritone is slightly too large to continue the sequence. This “broken” series of fourths is a prominent melodic figure in Movement II, creating another connection between the Toccata and the Canzone.
Movement II makes elaborate use of a harmon mute by asking the player to dynamically remove and replace the mute by varying degrees. The mute has the function of dampening the lower frequency spectrum and strengthening the higher partials of the sound, creating a softer, metallic tone. Removing the mute restores the lower frequency components and increases the overall volume. The general effect of the mute is a coloristic emphasis on certain pitches. In a somewhat opposite manor, Henze asks the player to use a wide vibrato on marked notes so that the pitches become obscured by smearing. Using these extended techniques and note length as a guide, one can isolate pitches that are emphasized due to coloristic effect or long duration. Example 9 shows many of these pitches and the relationships generated by them:
EXAMPLE 9: Pitch structure based on note emphasis in Movement II from Henze’s Sonatina for Solo Trumpet.
The pitches selected in Example 9 are subjective to a certain degree. Midway through the first line, for example, the mute is partially removed between an A♮4 and a B♭4. A case can be made for emphasis on one pitch or the other. I have chosen the B♭4 over the A♮4 due to its placement at the end of a phrase and its slightly longer duration.
Conceding the subjective choice of pitches, I think some large-scale formal connections can be made using atonal set classes. Due to the prevalence of sc(016) on the surface, one would assume that it also plays an important role in the background. Example 9 shows that this is at least partially the case. Other important set classes found on the surface are also found in the background. These have been previously discussed and include sc(015), sc(025), and sc(027). Based on these findings, I propose that sc(016) is working in a background layer as structural moments using pitch classes E♭, B♭, and E♮. In addition to the previously mentioned coloristic effects and note length, I believe that these pitch classes in particular have been marked for memory due to dynamic level, accent, and repetition. It is also important to note that the movement begins and ends on E♭5 (respelled to D♯5 for the last note). In a way, this structural progression based on sc(016) describes a movement away from, and back to, the point of origin.
MOVEMENT III
The musical language of the last movement, entitled “Segnali,” while stylistically similar to Movement I, is compositionally much stricter than any of the preceding material. Movement III exhibits a 12-tone row in its first twelve notes, followed by more or less standard permutations of that row. I will start by discussing the properties of the row and their connection with the previous movements before demonstrating the idiosyncrasies of its implementation. Finally, I will offer some theories on the importance of sc(016) and address the problem with the final row.
The first twelve notes of Movement III constitute the prime form of the row. Example 10 shows the matrix derived from the row and some of the row’s salient properties:
EXAMPLE 10: Properties of the 12-tone row in Movement III from Henze’s Sonatina for Solo Trumpet.
One of the first aspects to notice about the row in its context is that it is interrupted by a fermata between ordinals 10 and 11. This interruption indicates that full row statements are independent of phrasing. In a subtle way, it also shows that ordinal 10 holds a special function that will be revealed later. Further investigation into the row’s properties show that there is a predominance of ic5 among unordered pitch class intervals. This sequence of intervals has a strong connection with the previously mentioned series of ascending fourths present in both preceding movements. In addition, the tritone between ordinals 9 and 10 mirrors the “broken” series of ascending fourths also occurring in Movements I and II. Relevant set classes like sc(016), sc(025), and sc(027) can be constructed by subdividing the row into trichords. In summary, the row is packed with materials that have already been at work in the previous movements.
Using the 12-tone matrix, one can plot a path of permutations across the entire third movement. However, some issues begin to emerge that signal that this is not a serial work from the Second Viennese School. Those issues are ordinal position switching, out of order repetition, missing pitches, and the problematic final row. Example 11 presents the sequence of row permutations in Movement III showing some of these issues in context. Note that switched ordinals are indicated by double-headed arrows and that missing pitches include their ordinal number and pitch class:
EXAMPLE 11: Serial permutations in Movement III from Henze’s Sonatina for Solo Trumpet.
The second full row statement is a repetition of P11, only this time ordinals 9 and 10 have been switched. With the exception of the following row, P6, and the final row, all remaining permutations have ordinals 9 and 10 switched. In the case of retrograde or retrograde-inversion, the corresponding ordinals, 3 and 4, are switched. This decision to switch members of the row around ordinal 10 might have been indicated by the fermata interruption in the first line. It is notable that the interval between ordinals 9 and 10 is a tritone. Taking each of these tritone pairs, one can plot a path through the row permutations. Example 12 elaborates on the nature of this sequence of successive tritone dyads:
EXAMPLE 12: Row ordinals 9 and 10 as a tritone progression in Movement III from Henze’s Sonatina for Solo Trumpet.
The ordering of row permutations so that tritone dyads are related by semitone appears systematic. There are three interruptions of this semitone cross relationship, each occurring at a musical interruption. When represented horizontally to show contour, it is clear to see a distinctly ascending shape in the tritone dyads rising from sc(17), to sc(28), and ending on sc(39).
The final row of Movement III is incredibly problematic. Starting on the repeated B♮5 in the second to last system, these thirteen notes (D♮5 is repeated) only remotely resemble permutation R10. Major changes have been made to each hexachord of the row as shown in Example 13.
EXAMPLE 13: Transformation of R10 into the final row in Movement III from Henze’s Sonatina for Solo Trumpet.
The first hexachord contains three odd numbered ordinals in their correct location with the even numbered ordinals rotated to the left around them. The second hexachord is mostly intact after a rotation involving the last five ordinals. This version of “R10” is on the verge of being unrecognizable and appears to be intentionally manipulated so that it emphatically marks the end of the piece. While many of the previously discussed set classes and interval classes are embedded in the final row, any further connections to this or any other movement are tenuous.
Several important connections can be made between sc(016) and portions of Movement III. One of the stylistic features present in both Movement I and Movement III is the use of a compound line. In order to effectively maintain the perception of a compound line, Henze uses large, disjunct leaps from the high to low register. Upon separating the compound line, one finds several instances of sc(016) as shown in Example 14:
EXAMPLE 14: Compound lines as interlocking groups of sc(016) in Movement III from Henze’s Sonatina for Solo Trumpet.
The existence of so many instance of sc(016) on the surface of Movement III prompts the question of composer intention versus relationships inherent in the row. I believe that these groups of sc(016) are intentional due to their interlocking, compound construction. As revealed above, adjacent ordinal relationships inherent in the row do yield some sc(016) trichords, but not enough to create the density shown in Example 14. Therefore, the presence of such a proliferation of sc(016) in Movement III’s compound line proves composer intention in using the atonal set class.
CONCLUSION
The aim of the discussion up to this point was to tie the three movements of Henze’s Sonatina for Solo Trumpet together under the overriding mechanism of sc(016). I have argued that the Sonatina is an example of subordination. The tonal and serial language present in the piece is ultimately organized through atonal set classes. However, even with the presence of sc(016) on some level in every movement, this argument for cohesion is admittedly imperfect. Unfortunately, no all-encompassing statement of sc(016) appears to drive the piece. This post-Webern, post-Darmstadt composition exhibits an unsurprising degree of convolution involving its construction. In order to reconcile the apparent disparity left at the end of this study, I have offered below some alternative hypotheses connecting the three movements.
One way to draw a through-line from Movement I to Movement III is by looking at the highest pitches as they progress through the piece. Example 15 shows the highest pitches in each of the three movements:
EXAMPLE 15: The highest pitches of each movement in Henze’s Sonatina for Solo Trumpet.
The chromatic ascent from C♮6 in Movement I to the D♯6 in Movement III is a simple, yet clear way of communicating a progression through the Sonatina. The entire piece can be thought of as a rising expansion of the pitch space, generating a climax at the highest pitch, which also happens to be the last note.
Another theory of cohesion would be to elaborate on the series of ascending fourths explained in detail above. Sequences of ic5 and ic6 can be found in each of the three movements as illustrated in Example 16:
EXAMPLE 16: Sequences of ic5 and ic6 in Henze’s Sonatina for Solo Trumpet.
Movement I has a large, uninterrupted series of ic5 in the first phrase. This is soon imitated in phrase 2 and truncated with the aforementioned “broken” series containing ic6. Movement II has several short statements of ic5 with an ic6 ending. Movement III has some instances of the “broken” series due to its presence in the row. The piece ends with a series of ic5 ending with a surprising ic4. This motive, appearing in all the movements, seems to convey the idea of expansion and contraction around the perfect fourth. A closer examination of the work’s dyads would likely reveal a complex array of expanding and contracting intervals around ic5.
Another theory of cohesion would picture each movement as sharing some but not all compositional features with the other movements. A network of relationships is suggested in Example 17:
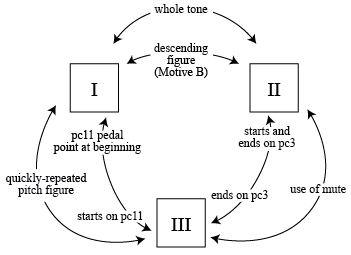
EXAMPLE 17: A network of relationships between the movements of Henze’s Sonatina for Solo Trumpet.
This suggested network contains several features like whole tone sonorities and pedal points that have been described in detail above. Starting and ending pitches listed here also provide a way to link the movements together. This type of network is coarsely generalized in Example 17, but it could provide a starting point to a study of mutually exclusive cross-relationships in the movements of the Sonatina.
I would be remiss if I did not mention the tantalizing possibility that the 12-tone row in Movement III is at work in the other two movements. The search for such a cohesive process was not fruitful in this study. Perhaps a new perspective borne from the present research might lead to a revelation regarding this alluring connection.